A mantra we hear all the time in security is the notion of defense in depth. It's applied in numerous areas from protecting computer systems to safeguarding airports. Anyone who receives formal training in security will likely encounter the term at least once in their coursework. It's a milestone we are told to strive for when designing secure systems.

For readers who are unfamiliar with the term, it's the idea that when designing security into a system, we should place several overlapping layers of defense wherever possible. The insight behind this idea is that thwarting an attack only requires one layer of defense to succeed whereas the attacker's success depends on penetrating every layer. Consider, for example, an invading army storming a castle. In order for the invasion to succeed, the invaders must survive raining arrows from archers, traverse a moat, breach the castle walls, and kill the soldiers inside. Failure to surmount any one of these defenses spells disaster for the attack. Worse yet for the invading army, as long as each layer's chance of successfully halting the attack is independent from the other layers, adding more layers makes the attacker's task more likely to fail. On the other hand, this is great news if you are the one assigned to defend the castle.

Unfortunately, step outside the classroom and it will not take long to run into the counterforce that stifles an otherwise brilliant concept. The force I am referring to is economics. Defenses don't come for free and as I plan to highlight in this blog post, there is a fundamental problem with applying defense in depth once economics enters the equation.

To aid my explanation, let's use fair coin flips as a simple running example. Although coins are a far cry from airports or castles, the underlying probabilities behind flipping a coin are simple to understand and also sufficient to make my point.

As you are probably already aware, a fair coin flip yields one of two possible outcomes, heads or tails, with equal and mutually exclusive probabilities. The probability of getting heads once is 50%. Getting heads twice in a row is 25%. Three times is 12.5%. This probability p is expressed by the following formula for x coin flips:

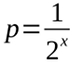
If we graph this function for a couple of flips, we get the following figure:

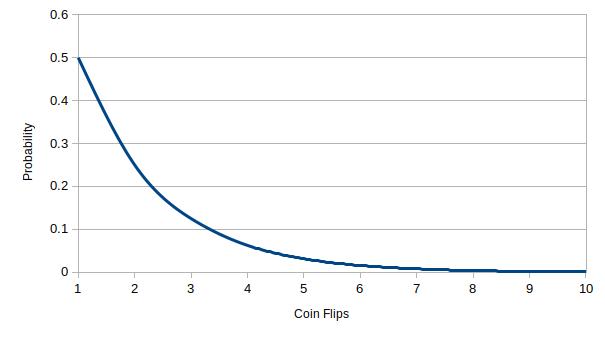
As we can see, the relationship between the number of flips and the probability is exponential. Adding a few additional flips significantly impacts the probability of getting all heads at first, but as even more flips are added, eventually the effect diminishes. In other words, the difference in chance of getting two heads verses three is substantial, but the difference between 999 and 1,000 heads is comparatively minuscule. Tying this analogy back to security, if we map the outcome of heads to the attacker successfully breaching a layer of security, we can see how overlapping a few defensive layers can offer significantly better security and reduce the attacker's chance of success. However, with each additional layer, the defender's gain diminishes. Regardless, this outcome shows that defense in depth is fundamentally valuable and we can safely apply it in the real world as long as the effectiveness of the layers being evaluated are completely (or at least nearly) independent to each other.

Unfortunately, as I alluded to in the introduction, every layer of defense has a cost to design, implement, deploy, and maintain. If these costs are also completely (or at least nearly) independent, a problem arises. Namely, each additional layer raises the cost of the overall defense linearly, but the return yielded in security diminishes exponentially. Returning to our running example, now consider the case where each flip costs one unit of resource to perform. If we add this function to our previous graph, we get the following figure:

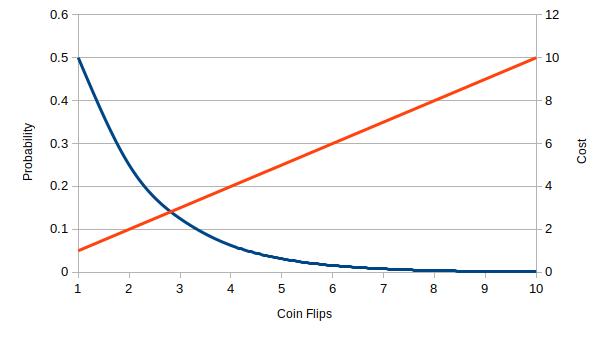
And if we reformat this graph to show the proportional gain in cost to the gain in security, we get:

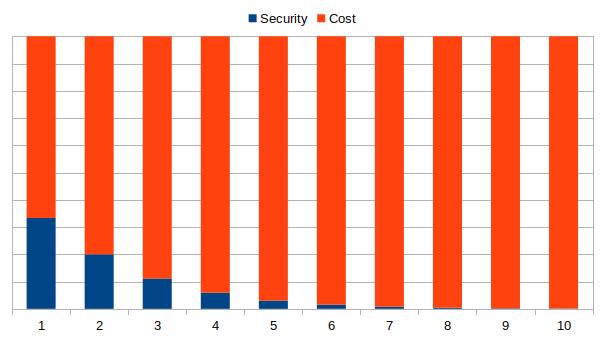
Put plainly, the cost of using defense in depth to achieve decent security is relatively cheap, but achieving exceptional security is extremely expensive. This is bad news for the defender and a fundamental limitation to the idea of defense in depth.

Hopefully you now understand the title of this blog post and realize why this relationship is important to grasp. For example, understanding this topic helps explain the controversies and debates surrounding the cost of funding the Transportation Security Administration's twenty "Layers of Security" framework:

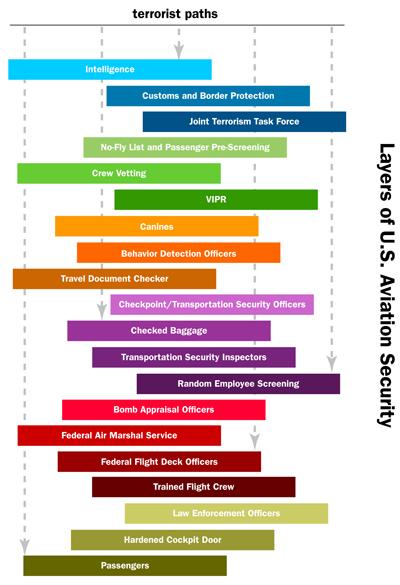
I'll forgo an in-depth analysis of this chart since other researchers have already examined it in great detail, but to summarize, if you pick a relevant threat to airport security and consider each layer's effect on stopping it, you'll realize removing any one layer has seemingly little impact on the overall risk of failure. This begs the question of whether there are layers that can be removed to significantly reduce cost without significantly reducing security. Certainly an idea worth exploring, if the science can be separated from the politics. Until then, I hope you've found this blog post interesting and insightful.